With our algorithms we make impossible problems tractable.

A Playful Example
There are 10249 possible moves in a game of Tic-tac-toe (played in three dimensions on a 6 by 6 by 6 board).
There are not enough atoms in the universe to represent all possible moves in that game!
We built mathematical tools to reduce the size of the game tree (which represents all possible moves in a game of Tic-tac-toe). This smaller game tree could then be searched by modern computers to answer questions like: can the second player force a draw in a game of Tic-tac-toe.
The idea is best illustrated by the use of examples. Consider the complete game tree of the 2x2 Tic Tac Toe board –
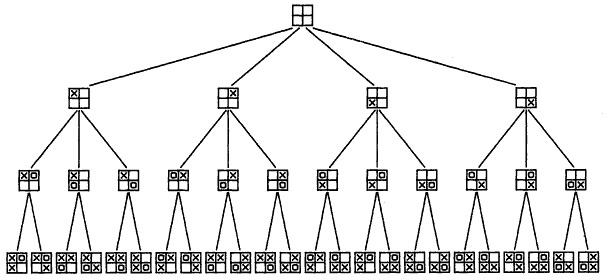
We immediately see that the four boards in the second row are all equivalent since for player X all four positions are equivalent (It does not matter which corner of the game you pick to start the game. Keeping this equivalence in mind we can shrink the game tree to (Figure 2):
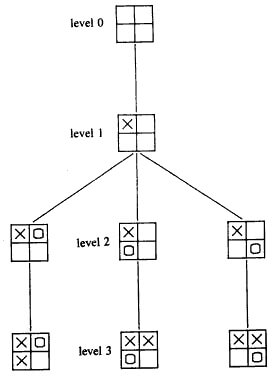
Figure 2

Figure 3
Finally we note that at level 2 the last two boards are equivalent to the first one. The reasoning here is a bit more tricky. The idea is that you can take a board and change it to some other state as long as you maintain all the Tic Tac Toes (all possible lines e.g. XX, 00 etc.).
The intuitive idea of equivalence is embodied in and central to Automorphism Groups. One can think of Automorphisms as the set of all boards that are equivalent to each other. The problem that the mathematician is faced with is to generate that Group. How do you do it?! The problem can be solved by noting that:
- We can do something (e.g. rotate- 0,90,180,270 degrees or flip along horizontal, vertical, diagonal axis) to the board and still keep all Tic Tac Toes intact.
- We can move certain positions of the board in a special way (e.g. on a 4x4 board exchange all the centers with the corners) and still maintain all Tic Tac Toes.
The important observation here is that there are two classes of automorphisms. The ones where individual adjacent squares in the board are moved around (so that they are no longer adjacent to each other) to create an automorphism and in another where adjacency is maintained (for example a flip along the diagonal will preserve adjacency). The former can be generated by the symmetries of the board and the latter though a special algorithm (to be described later).
Once we know the Automorphisms we can rule out equivalent boards from the search tree. To give an example: In the 4x4x4 board we can cut down the initial (first three moves) tree size from 64x63x62 to 1x7x1. We effectively reduced tree size by a quarter of a million. In the 6x6x6 case we cut down the size by nearly 3 million game boards using just one class of group automorphisms. In fact, using such tools we can reduce/prune the game tree of the 6x6x6 Tic-tac-toe from 10249 to 108.


